Probability and Statistics in C++: Dice Rolls

Now that we have learned the basic concepts of Arrays in C++, we will see a use in their practice, making data entries and using Probability and Statistics concepts.

Dice rolls in C ++

What we are going to do is very simple: we are going to roll dices, that is, draw numbers from 1 to 6.
We will do this 100 times, 1000 and 100 thousand times.

Initially, we declare an array of 6-position 'dice' name, of the integer type, and initialize with a null value. We will use an integer num to store the generated random number.

Then, to generate the numbers, we will use the gen() function:

int gen()
{
    std::random_device rd;
    std::mt19937 gen_numb(rd());
    std::uniform_int_distribution<> dis(1, 6);

    return dis(gen_numb);
}

We use a more sophisticated solution, as we will generate thousands of random numbers, in a very short time, and for that the rand()/srand() would not do (generate a lot of numbers).

We will use the raindon library and it will return an integer between 1 and 6, simulating a given.(Reference: https://en.cppreference.com/w/cpp/numeric/random/uniform_int_distribution)

If it comes out 1, we store in position dice[0].
If it comes out 2, we store in position dice[1].
...
If it comes out 6, we store in position dice[5].

Now, just do: num = gen();
Then: dice [num-1]++ (since the array ranges from 0 to 5)
And increment the 'num' index of the array by one.

We make the loopings run, first generating the random ones, then showing how many times each number came out (the number 'num' came out dice[num] times). Do not forget to reset the values of the array, before each loop of number generation.

See how our code looks:

#include <iostream>
#include <iomanip>
#include <random>
using namespace std;

int gen()
{
    std::random_device rd;
    std::mt19937 gen_numb(rd());
    std::uniform_int_distribution<> dis(1, 6);

    return dis(gen_numb);
}

int main()
{
    int dice[6] = {},
        num=0, aux;

    cout <<"100 dice rolls:"<<endl;
    for(aux=0 ; aux<100 ; aux++){
        num = gen();
        dice[num-1]++;
    }
    for(aux=0 ; aux<6 ; aux++){
        cout<<"Number "<<aux+1<<" cames out: "<<dice[aux]
            <<" ("<<fixed<<setprecision(2)<<100.0*dice[aux]/100<<" %)"<<endl;
    }

    cout <<"\n1000 dice rolls:"<<endl;
    for(aux=0 ; aux<1000 ; aux++){
        num = gen();
        dice[num-1]++;
    }
    for(aux=0 ; aux<6 ; aux++){
        cout<<"Number "<<aux+1<<" cames out: "<<dice[aux]
            <<" ("<<fixed<<setprecision(2)<<100.0*dice[aux]/1000<<" %)"<<endl;
    }

    cout <<"\n100000 dice rolls:"<<endl;
    for(aux=0 ; aux<100000 ; aux++){
        num = gen();
        dice[num-1]++;
    }
    for(aux=0 ; aux<6 ; aux++){
        cout<<"Number "<<aux+1<<" cames out: "<<dice[aux]
            <<" ("<<fixed<<setprecision(2)<<100.0*dice[aux]/100000<<" %)"<<endl;
    }

}

We could have done it directly with the code: dice[gen () - 1]++
It's the result:

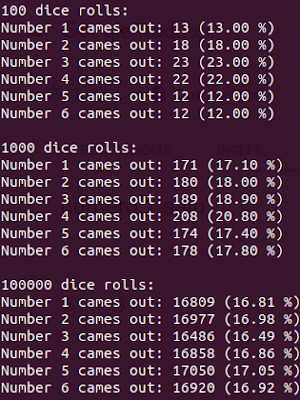
According to the theory of probabilities, the chance of getting some number on a die is 1 in 6, or 1/6 or 16.67% of chances.

Note that in 100 releases, the result is a little fluctuating.

As we increase the number of rolls, the actual statistics will approach the result of the theory, around 16.67%, so our method of playing dice is more and more realistic and more random as we increase the number of launches .